M.Arch Thesis: Our Lady of Lourdes and the Waters of Life – Architecture and Geometric Representation
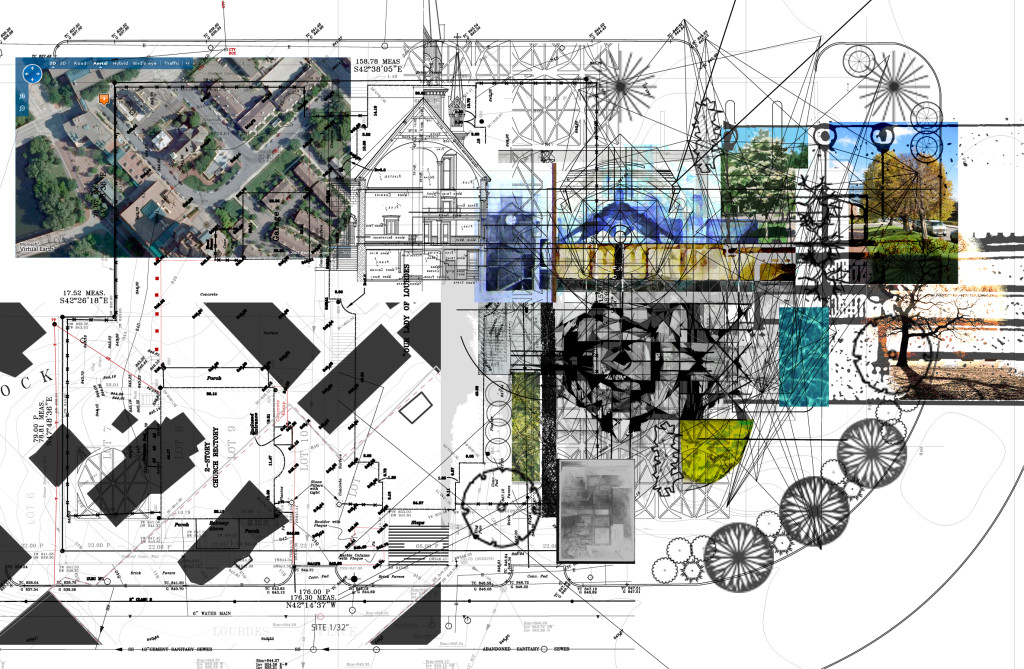
Architecture and Geometric Representation: Our Lady of Lourdes and the Waters of Life
Euclid’s famous geometrical text Elements, written 2,500 ago is still of vital importance to architectural design and the construction of buildings, but our attitudes about geometry have shifted greatly since formulation. In his article “The Invention of Space,” F.M. Cornford speculates on who is responsible for misleading society for so long, causing people to assume that Euclidean Space was actually the correct way to describe the world we live in. With the appearance of other geometries and the theory of Relativity, Cornford and others are forced to wonder about our historical knowledge in relationship to geometry. He says, “If the infinite extent of three-dimensional space is no more than a construction of the human brain and only one of many possible alternatives, all equally agreeable to nature, when and by whom was it constructed?”[i] The very essence of the idea presented is emblematic of society’s reflex to assume that truth in science is infallible, and therefore anything opposed to it false. There are many examples of the problem with this attitude including the case of missing neutrinos, dark matter, and Einstein’s cosmological constant, which show that science is always a mode of speculation and never 100% accurate.[ii]
Unfortunately, mathematics and science have fallen prey to the absolutism and certainty that has become a common theme in many aspects of our lives. Even worse, these rational systems, along with technology, have become dominating forces that have determined thought and action in society and architecture. Thus, we live in an age where man has the illusion that Truth is demonstrable through the laws of science and existential questions are avoided at all costs; yet the very essence of architecture is philosophical.
My thesis began by asking, what is the relationship between geometry, astronomy, and architecture? My initial assumption was that the clearest way to manifest this relationship would be to design a planetarium, or a house for a telescope. My research into this relationship continued to bring me into pre-modern understandings of space where geometry, astronomy, and architecture were linked through the study of ontology. This interest in the nature of being is still fundamental to contemporary understandings of geometry, astronomy, and architecture, and was the catalyst in determining the site and program for this project. What is at stake is related to questions about life, death, and the meaning of existence. In light of this I chose to work with the Church in our society, as it is an institution that works to address these questions in our time.
The initial inspiration for this project came from the recent destruction of the grotto on the façade of the Our Lady of Lourdes in Minneapolis. I asked what role could a grotto environment play in our modern secular society, how can this space connect to the surrounding community of gardens and parks, and how can design bring public presence to the oldest continuously used church in Minneapolis? As a metaphor for the cosmos, the grotto is by its very nature vague and lacking in definition; yet, the presence of water – actual or implied – is the defining characteristic of the grotto. The word grotto is derived from the Latin crypta meaning a concealed subterranean passage, a vault, cavern, cave, or pit.[iii] According to Naomi Miller, “the grotto is, above all, a metaphor of the cosmos.”[iv] One can therefore easily relate such architecture to ideas surrounding ontology and sacred geometry. Considering this, I was interested in a architectural project that was situated around the spatial experience of the grotto where the natural environment is used to intensify and enrich sensory perceptions. Simultaneously, the space was imagined as a place of surprise and wonder.
Considering water, it is important to understand the significant difference between the chemical nature of water, what it is made of, and its impact on our imagination and relationship with the “nature” of the world. Water exists and is manifest on many levels of understanding; in this project I was interested in the way that a unification of water and urban space could have moral and psychological consequences. These waters are elusive, difficult to grasp, and full of mystery. It is not the physicality of water that we strive to address but that which is found in dreams and the space of imagination. Water inherently contains metaphors of opposition; it is simultaneously a mirror that reflects and a deep abyss that hides that which lies beneath. Water is the source of all life and the substance from which all things originate; scientifically and spiritually. Not only do theories of evolution credit water with the formation of life but almost every creation myth is rooted in the division of the great waters of life.[v] Thus, this project was interested not just in the physicality of water found in the site’s relationship to the river but also the water of dreams and imagination. This analysis led me to wonder about the unification of water and urban space and consider if it could have moral and psychological consequences, which ultimately led to the decision of creating a baptistery for the church.
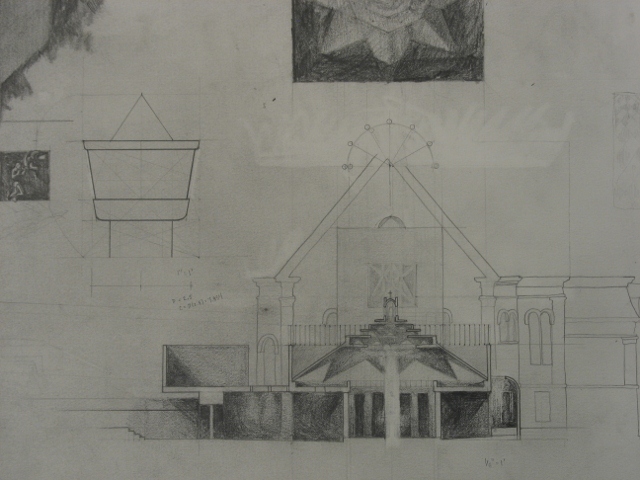
The theology surrounding baptism indicates that it is a sacrament that is a mystical imitation of Christ’s death, burial, and resurrection.[vi] My project used this understanding to design a space that speaks to this experience. First and foremost in the creation of such an environment was the consideration of light. Specifically, I was interested in indirect light, coming from an unknown source where its materiality is revealed through its interaction with stone and water. Simultaneously, darkness allowed the light to become inspirational and sets up the ideas surrounding death and rebirth. Direct light is considered only for special occasions and the building is orientated to allow direct light to hit the font on and near Easter, the day associated with Christ’s rebirth. The parking garage on the south side was also a consideration because, through its adjacency and violent use of the landscape, it takes away from the sacred quality of the site. This became the location of the profane waters that are available to the greater community as a grotto garden.
The most basic way to understand light, representation, and process in this project was through the use of a pinhole camera. This camera uses no lens, so it is the actual light imprinting the image on the paper. The cylindrical geometry of the oatmeal box creates a specific geometric projection that represents the world in ways that are otherwise impossible. These photographic studies were essential in understanding the placement of the baptistery on the site. Meanwhile, the lengthy and complex process of obtaining the actual image informed my design process.
Because I am concerned with the experience of the place and the role of the sacred in architecture it became apparent that the tactile experience of physical drawing, models, and interpretation of those things through photography was appropriate to this project. These drawings represent an exploration into the role of the baptistery in the church, its relationship to the larger community, historical symbolism, and the design of a religious experience. They are a collection of revelations and experiments into the creation of this architecture. Within each, one will find questions regarding history, spirituality, and the nature of being. All are attempts at understanding questions regarding this exploration and can be seen as attempts to understand the relationship between geometry, astronomy, and architecture. Thus, drawings explored the experiential quality of the baptistery, its relationship to the church, orientation to solar, lunar, and celestial events, and role of levels in the architecture; meanwhile, photography set up the idea of process and superimposition; while models began to make these ideas physical.

Geometry, Astronomy, and Sacred Meaning
Geometry (to measure the earth) can be traced back to the very origins of architecture as a mediator between the celestial and terrestrial. The very nature of its study involves forms, shapes, and space, all of which are inherent to understanding architectural design. At the same time, geometry is considered one of the oldest sciences and was first put into axiomatic form in 300 B.C. by Euclid, whose mathematical theory became the standard for the following 2000 years. Although marred by contradictions and gaps, the Elements, became an immensely useful text for all the fields where geometry was applied. Optics, mensuration, surveying, navigation, astronomy, agriculture, and architecture all benefited from the newly established rules of geometry that allowed for the solving of problems.[vii]
The field of Astronomy, specifically the mapping of the stars and planets on the celestial sphere, served as the proving ground for geometric problems. This geometric understanding was the model for correct reasoning until the middle of the nineteenth century when non-Euclidean geometries were discovered.[viii] Therefore, architecture, concerned with the making of forms, greatly profited from the knowledge put forth in the Elements. Vitruvius, Christopher Wren, and Le Corbusier all understood the world through the geometrical lens of Euclid. It is true that other branches of geometry, which arose after the seventeenth century, affected architecture, but this can be considered minor in relationship to the impact of Euclid on the history of building. In fact, the influence of projective geometry or multidimensional space on architecture is relatively minor in comparison.[ix]
Because of this, understanding geometry is essential to the education of an architect. On this topic, Vitruvius says, “Let him be educated, skilful with the pencil, instructed in geometry, know much history, have followed the philosophers with attention, understand music, have some knowledge of medicine, know the opinions of the jurist, and be acquainted with astronomy and the theory of the heavens.”[x] He then goes on to say that geometry is important because it allows the architect to make plans, consider optics, and solve difficult questions regarding symmetry.[xi] Vitruvius also emphasized the importance of geometrical understanding as expressed in astronomical knowledge because it allowed the architect to “find the east, west, south, and north, as well as the theory of the heavens [mathematical and musical harmony], the equinox, solstice, and courses of the stars.”[xii] Geometry then plays a fundamental role in how an architect creates a place in the world.
Although seemingly pragmatic, this prescription by Vitruvius holds significant philosophical value as well. We know that Plato was very interested in geometry, and Vitruvius gives one of Plato’s theorems, on the doubling of a square.[xiii] In this theorem, one is given a square and asked to double it; figure 1.4 shows how this could be done. The proof is that exactly double of the original square is in the four triangles, each of which is congruent (identical) with a triangle that is one fourth of the original square. Vitruvius states that, “Nobody can find this by means of arithmetic,” referring to the discovery of irrational numbers. Thus, if the sides of a square are of unit length, the length of the diagonal cannot be expressed as a rational number, that is as a fraction p/q, where p and q are integers.[xiv] Hence, Vitruvius is stating that the geometrical construction allows one to easily obtain that which can not be found with any other method because a numerical solution would always be an approximation. The philosophical tie is situated in the fact that the immeasurability of an irrational number is related to the transcendent nature of God.[xv]
This metaphysical link between geometry and God is found in classical education. Geometry, arithmetic, and astronomy constituted the major intellectual disciplines of one of the two divisions of classical education, while the fourth element of the Quadrivium was the study of harmony and music. The laws of harmonics were considered unchanging and universal elements that defined the relationship between the heavens and the earth, and the practice of geometry was a way to understand the ordering of the cosmos. According to Robert Lawlor,
The implicit goal of this education was to enable the mind to become a channel through which the ‘earth’ (the level of manifested form) could receive the abstract, cosmic life of the heavens. The practice of geometry was an approach to the way in which the universe is ordered and sustained. Geometric diagrams can be contemplated as still moments revealing a continuous, timeless, universal action generally hidden from our sensory perception. Thus a seemingly common mathematical activity can become a discipline for intellectual and spiritual insight.[xvi]
Thus, the tactile experience of creating geometry allows the human body to become a channel for cosmic energy and spirituality and a way to reveal that which is hidden from our senses. Plato gives support for this philosophical position when he considers geometry as the most essential form and ideal philosophical language.[xvii] In fact according to Plato:
[the geometers] make use of the visible forms and talk about them, though they are not of them but of those things of which they are a likeness, pursuing their inquiry for the sake of the square as such and the diagonal as such, and not for the sake of the image of it which they draw. And so on in all cases…What they really seek is to get sight of those realities which can be seen only by the mind.[xviii]
For Plato, Reality consists of pure essences or archetypal ideas and one is only capable of perceiving their pale reflections. In this passage, Plato clearly recommends geometry as the model by which one should describe the metaphysical realm. The Platonist sees this geometrical understanding as innate in oneself, acquired when one’s soul was in contact with the realm of ideal being.[xix] This relationship between harmony and geometry is also seen in an example given by Sebastiano Serlio in the first of his Five Books of Architecture (figure x), where he gives a geometrical scheme for the laying out of a door.[xx] This division of a square into three parts coincides with a harmonic sequence by setting up a process by which one can divide any rectangle into perfect ratios of the original. If the process is continued it establishes a harmonic sequence that divides the rectangle into perfect proportions.
Geometry and Astronomy then, are not simply used as tools, but provided rich ground for architectural meaning. The poetic substance of this meaning has always been situated in the realm of sacredness because scientific inquiries are primarily ontologically motivated. Such is true, so that asking questions about the nature of the cosmos and interpreting observations through the lens of geometry presupposes a human dimension; all is in reference to both human experience and scale and the harmonious geometry of the cosmos is found in the proportions of the body.[xxi] Architecture then, uses this understanding in an attempt to create order in the seemingly unordered cosmos. It is through this geometrization of our world that we have attempted to establish a place on the earth. Indeed, the myths of the origins of architecture require such geometrical modes of thought.[xxii]
Sacred geometry’s potential has not been exhausted. It allows for infinite variation, unlimited design potential and can be used without copying the forms of the past, which have successfully used these geometries to create meaningful architecture for over 3000 years. The use of these geometries allow for symmetry (in the Vitruvian sense) between architectural components, which leads to structural firmness, ease of construction, decreased cost, and everlasting beauty. These forms contain inherent beauty and symbolism and allow for an architecture that is in relationship with the spiritual nature of our being.
Throughout this thesis, I am using modern science, including astronomy and mathematics, as an example of the shift between logic and spirituality – indeed exemplifying the division between sacred and profane – as a critique of modernist assumptions that we must discard the past and find a completely new spirit. This attempt has led us down the path to materialism and consumption and away from the nature of humanity. Indeed a return to our essence through sacred geometry is a step toward a new future without discarding the past and simultaneously formulating an architecture that speaks to a 21st century understanding of our place on the earth and under the heavens.

Scientific Skepticism and the Nature of Truth
Science is founded on axioms of truth. In order to prove a logical statement true or false one must begin with a set of rules called axioms. One holds such statements true for all questions within a set of objects. Take for example, the concept of parallel lines. According to Euclid, two lines are parallel if, and only if, they never intersect. In his 5th postulate:
That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.[xxiii]
More simply put, all triangles add up to 180 degrees. This however is not a true or necessary axiom. In fact, only some do, and other geometries have been developed without this assumption. They prove to be equally and arguably more compatible with the observed universe. It was the spherical geometry of Riemann that allowed for the development of the theory of relativity.
Yet, spherical geometry is largely based on Euclidean geometry as it is still assumes the first 4 axioms. Likewise, it would be simple to assume other postulates in the method of addition and show that 1 + 1 does not equal 2. The logic of a base 12 counting system begins to show how this might work; a lunar calendar or even the zodiac science are further examples.
Even with the advent of the supercomputer it is impossible to determine which geometry is truly descriptive of our universe because of the margin of error in any physical measurement. How then does one define or determine which geometry is most relevant to the interpretation and creation of architecture?
Geometry is developed from ontological questions and interconnected to premodern man’s understanding of spirituality or God. This connection has been lost in contemporary society through the discovery of modern scientific revolutions that contradict the spiritual nature of man, which has put architecture, concerned with both branches of knowledge, into a crisis. Contemporary man finds himself in the ruins of modernism, convinced by progress, but living in profanity – a space where the shopping mall has become the new Sunday destination.
The history of science has shown us continually discarding and revising world views to fit within the current paradigm. Anything that does not fit within this world view is ignored or altered to fit the paradigm. Advancements in knowledge concerning the nature of the universe and man’s place in the cosmos have created a social attitude that somehow space is describable through science and reason. With this, humanity has never before seen the “progress” that is being witnessed in our time. Yet, inherent in this progress comes a crisis that is connected to the nature of truth and the seeming infallibility of science. According to Husserl, the beginning of the crisis coincides with the end of classical geometry and the appearance of non-Euclidean geometries, which occurred near the end of the seventeenth century.[xxiv] At this time, architecture and geometric representation shifted and a division was created between science and spirituality.[xxv]
One reason for this is because advancements in knowledge and rational thinking began to contradict faith and spirituality.[xxvi] A new way to think about geometry and its relationship to architecture began to emerge. Mathematics and astronomy were no longer valued for their ability to mediate between the physical world of man and the realm of poetics but instead their capacity toward Reason.[xxvii] This shift is partly responsible for what Mircea Eliade calls the “desacralization of the cosmos.” He says, “the completely profane world, the wholly desacralized cosmos, is a recent discovery in the history of the human spirit…it is enough to observe that desacralization pervades the entire experience of the nonreligious man of modern societies and that, in consequence, he finds it increasingly difficult to rediscover the existential dimensions of religious man in the archaic societies.”[xxviii]
Interestingly, many claim that non-Euclidean geometry provides the new way of understanding the world. Indeed, this is true to an extent, but only because it allows for a new mathematical representation of the cosmos, not because it redefines our world order. Both geometries are founded on assumptions about the world and show us ways to understand our place in the cosmos. The real beauty behind the formulation of new geometries is that it makes apparent the fact that initial assumptions lead to different results, and exemplifies a shift in our understanding of our place in the universe through a reevaluation of mathematical knowledge, what Thomas Kuhn calls a paradigm shift.
These shifts are not, however, a completely progress move; in fact, according to Thomas Kuhn, “An apparently arbitrary element, compounded of personal and historical accident, is always a formative ingredient of the beliefs espoused by a given scientific community at a given time.”[xxix] Scientific knowledge is based to a great degree on assumption and speculation. This fact reveals the necessity of careful choice in representation of ideas. For example, without a non-Euclidean representation of the cosmos Einstein would have never developed relativity; simultaneously, relativity must be considered with skepticism because the founding principles are not necessarily fact but only assumed true for a specific situation.
This divide is closely related to the loss of meaning in architecture and can be considered in light of the cataclysmic change in the nature of society and ways of thinking in the birth of enlightened thought. It is important to consider that many of the ideas formed at this time are still with us and according to Joseph Rykwert, “Disguised by their apparently rational and objective formulation, they are sometimes dangerously inhibiting. But ignorance of their true nature may often prevent us from forging them to our own use.”[xxx] The divide between science and spirituality is one such concept and the science of geometry can be seen as evidence of such a social shift because the symbolic relationship began to dissolve in the enlightenment with the implementation of logical reasoning and discovery of scientific theories that seem to prove spirituality false and illogical. One question that arises from such in inquiry is how does the unprogressive nature of scientific thought open possibilities for design in architecture?
Today, our Western, secular society, has faith in the ability of science and skepticism toward spirituality. For many it seems impossible for these frameworks of knowledge to be interrelated, especially in architecture. Indeed, according to Alberto Pérez-Gómez, “The assumption that architecture can derive its meaning from functionalism, formal games of combinations, the coherence or rationality of style…or the use of type as a generative structure in design marks the evolution of Western architecture during the past two centuries.”[xxxi] In fact, some have claimed that geometry and the meaning associated with it is somehow archaic and that our society ought to find new modes of designing.[xxxii]
Science attempts to uncover fundamental truths but is always in a state of speculation regarding the “truth” of any conjecture. Infinity, the universe, and non-Euclidean geometry provide the conceptual framework for the exploration by showing that mathematical knowledge is fallible; therefore that science and spirituality are not mutually exclusive ways of knowing. In fact, both rely on faith of some sort. This attitude toward science is in line with Einstein’s conception of scientific thought when he says, “The belief in an external world independent of the percipient subject is the foundation of all science. But since our sense-perceptions inform us only indirectly of this world or Physical Reality it is only by speculation that it can become comprehensible to us.”[xxxiii] Indeed, there is much beauty and mystery in mathematical knowledge. Where did such a complex system of understanding come from? Why does it seem to allow us to answer so many questions? What role does it actually play in our mortal lives, and how can it help to develop sacred space in a secular society?
Progress does occur in science but it is not a linear process and always depends upon a historical basis. For example, Non Euclidean geometries depend upon the principles of Euclidean geometry. Thus, the intellectual shifts related to geometry and astronomy and their contradiction of spirituality can in some ways be understood as constructed. It is not necessarily true that science and spirituality are opposing epistemologies. Although new scientific and mathematical discoveries have seemed to contribute to the secularization of society, it is evident that much mystery still exists within these ways of knowing. In fact, our most current understanding of science is bringing us full circle in our understanding of the interconnectedness of matter, thoughts, experience, and being.
Thus, what we know is not necessarily constructed but its infallibility should be questioned. Because of this, our cities and lives are becoming a place where man’s reason for being is to express a technological process rather than establish a meaningful existence in a finite world. According to Pérez-Gómez, “contemporary man lives with the illusion of the infinite power of reason. He has forgotten his fragility and his capacity for wonder, generally assuming that all the phenomena of his world, from water or fire to perception or human behavior, have been ‘explained.’” [xxxiv] We have gone to the moon and looked back at the earth, and even explained things like subatomic particles, which are so small they are impossible to fathom; yet all is still done with a level of uncertainty.
Such ideas are becoming more relevant when one considers the changing role of science in our world. Indeed, according to Lawlor, “within the existence of this divide, the most current understandings of science are beginning to show that our world is best understood through geometry, form, and proportion. Therefore, the ancient culture’s examination of reality through the metaphors of geometry and music was actually very close to our most contemporary science.” [xxxv] Because of this it is important to be critical of scientific assumptions and cultural influences that seem contrary to ones humanity and instincts.
The Question of Parallel Lines and Infinity
The discovery of new geometries occurred through the reevaluation of one of Euclid’s axioms of geometry. Specifically, mathematicians began to question his 5th postulate which states that given a line and any point P off that line, there exists only one line through P that is parallel to the given line – that is, parallel lines never intersect. Bolyai and Lobachevsky found different geometries by reevaluating this 5th postulate and discovered that, an infinite number of lines can pass through P that never intersects the line. Let us assume that the world is not infinite but rather it is finite and everything, the earth and universe, exists within a sphere. Then it is possible for an infinite number of lines to pass through P and never intersect the given line. The ramifications of this theory are that all triangles add up to less than 180 degrees.
Riemann, on the other hand, said that it is not necessary to assume that a straight line is infinite merely because we conceive it to be endless. It can be an endless curve for example. Imagine for example that all exists on the surface of a sphere. Then when we draw a straight line on a piece of paper what we are really doing is drawing something that has a small curvature, and the longer the line the more able we are to determine such curvature. How we think about this straight line all depends on how we actually imagine the surface we are drawing on. We commonly think of the paper as a flat plane but this is only a habit of thought, and not a physical necessity. In thinking that all exist on a sphere, it can be shown that even “parallel” lines intersect. Another ramification to this is that the sum of the angles of any triangle drawn on the sphere are greater than 180 degrees, and approach 180 degrees as one makes the triangle infinitely smaller.
All of this forces one to ask, which geometry actually represents our world and experience, and can we not definitely determine, by measurement or otherwise, which actually applies? According to Euclid the sum of the angles of a triangle is 180 degrees, Bolyai and Lobachevsky show it is less, and Riemann shows it is greater. The problem lies in the fact that all physical measurement is subject to error and does not allow us to rule out any of the geometries.[xxxvi] Although other geometries have been discovered, Euclidean geometry remains valid, just as Newtonian dynamics was not replaced by Einstein’s relativity but simply a redefinition for a specific situation.




















































































































































































Notes_________________________________________________________________________________________________
[i] Cornford, F.M. “The Invention of Space.” in Essays in Honour of Gilbert Murray. (London, 1936), 216.
[ii] Kuhn, Thomas, The Structure of Scientific Revolutions (Chicago: University of Chicago Press 1990) 111-135.
[iii] Miller, Naomi. Heavenly Caves Reflections on the Garden Grotto, (New York: George Braziller 1982), 8.
[iv] Ibid, 7, 11.
[v] The creation of the world through the waters of Apsu can be found in the Enuma Elish, the Akkadian creation epic, written about 1000 years before Genesis. The first chapter of Genesis seems to “retell” this story when the waters are separated into the sky above and the waters below. There are many other creation myths related to water and reference to some can be found in:
Illich, Ivan. H2O and the Waters of Forgetfulness (Berkeley: Heyday Books 1985).
[vi] Krautheimer, Richard, “Introduction to an ‘Iconography of Mediaeval Architecture,’” Journal of the Warburg and Courtauld Institutes, vol. 5 (1942), 26-7.
[vii] Sbacci, “Euclidism and Theory of Architecture,” Nexus Network Journal 3, 2 (2001) 26.
[viii] Garrity, Thomas A. All the Mathematics You Missed (Cambridge: Cambridge University Press 2002) 161.
[ix] Sbacci, Michel. “Euclidism and Theory of Architecture” 26.
[x] Vitruvius, The Ten Books on Architecture, trans. Rowland, (Cambridge: Cambridge University Press 1999) I.1.3.
[xi] It is important to note that in I.2.4 Vitruvius states that symmetry is “a proper agreement between the members of the work itself, and relation between the different parts and the whole general scheme, in accordance with a certain part selected as standard,” and is not defined as mathematical reflection across an axis.
[xii] Vitruvius, The Ten Books on Architecture, trans. Morgan, (New York: Dover Publications 1960) IX.10.10.
[xiii] Vitruvius, The Ten Books on Architecture, trans. Rowland, (Cambridge: Cambridge University Press 1999) IX.intro.4-5.
[xiv] Pedoe, Dan. Geometry and the Visual Arts (New York: Dover Publications 1976) 29.
[xv] The circle represents God because the circumference is not measurable as it contains л.
Vesely, Dalibor, Architecture in the Age of Divided Representation, (Massachusetts: The MIT Press 2004), 155. Also, Krautheimer, “Introduction to an ‘Iconography of Mediaeval Architecture,’” 9.
[xvi] Lawlor, Robert Sacred Geometry (London: Thames and Hudson 1982), 6.
[xvii] Ibid, 9.
[xviii] PLATO, Republic, VII, 510 d,e., quoted in Lawlor, Sacred Geometry, 9.
[xix] Lawlor Sacred Geometry 9
[xx] Serlio, Sebastiano, The Five Books of Architecture, (New York: Dover Publications 1982) 20.
[xxi] Pérez-Gómez, Alberto, Architecture and the Crisis of Modern Science (Cambridge: MIT Press1996), 3.
[xxii] Vitruvius, The Ten Books on Architecture, trans. Rowland, (Cambridge: Cambridge University Press 1999) II.1.1-8. Here the origins of architecture and the wood hut are discussed.
[xxiii] Euclid, Euclid’s elements of geometry, from the Latin translation of Commandine. (London : printed for Tho. Woodward, 1723), 22.
[xxiv]Pérez-Gómez, Alberto, Architecture and the Crisis of Modern Science (Cambridge: MIT Press1996), 5
[xxv] “A classic example of divided representation is the double standard of truth that has plagued the history of modern science and theology.”
Vesely, Dalibor, Architecture in the Age of Divided Representation, (Massachusetts: The MIT Press 2004), 177.
[xxvi] An example of this is that many were actually using astronomy and geology to determine the age of the earth and their findings were contradictory to the Christian biblical account. The verification by Galileo Galilei of the Copernican theory can be seen in this way. Galilei, Galileo, trans William A. Wallace, Galileo’s Early Notebooks: The Physical Questions, London: University of Notre Dame Press, 1977.
Kuhn, Thomas, The Structure of Scientific Revolutions (Chicago: University of Chicago Press 1990), 111-76.
[xxvii] Durand, Jean-Nicolas-Louis, Précis of the Lectures on Architecture, trans. David Britt. (Los Angeles: The Getty Research Institute Publications Program 2000). See this publication and further discussion in Pérez-Gómez, 1996 for a closer examination of how Durand represents such a change in understanding.
[xxviii] Eliade, Mircea, The Sacred and the Profane, trans. Willard R. Trask, (New York: Harper & Row 1959), 13
[xxix] Thomas Kuhn, The Structure of Scientific Revolutions (Chicago: University of Chicago Press, 1970), 4.
[xxx] Rykwert, Joseph, The First Moderns, (Massachusetts: MIT Press 1980), 1
[xxxi] Pérez-Gómez, Alberto, Architecture and the Crisis of Modern Science (Cambridge: MIT Press1996), 4
[xxxii] Krell, David F. “A Malady of Chains: Husserl and Derrida on the Origins of Geometry and a Note to the Architects of the Future,” (Architectural Design 1947 67: 5-6).
[xxxiii] Kline, Morris, Mathematics and the Search for Knowledge (New York: Oxford University Press 1985), 19
[xxxiv] Pérez-Gómez, Architecture and the Crisis of Modern Science, 6.
[xxxv] Lawlor, Robert Sacred Geometry (London: Thames and Hudson 1982), 1
[xxxvi] For a more detailed description of these events and explanations of these different geometries see Cooley, Hollis R. Introduction to Mathematics. (Boston, MA: Houghton Mifflin Company, 1937) 206.